Osama Abrar:
а¶Єа¶Ња¶∞а¶Єа¶Ва¶ХаІНа¶ЈаІЗ඙: а¶≠а¶∞а¶ѓаІБа¶ХаІНට බаІЬа¶ња¶∞ බаІБа¶З ඙аІНа¶∞ඌථаІНට а¶Іа¶∞аІЗ ඃටаІЛ а¶ЬаІЛа¶∞аІЗа¶З а¶Яඌථඌ а¶єаІЛа¶Х ථඌ а¶ХаІЗථаІЛ බаІЬа¶ња¶ХаІЗ а¶ЖථаІБа¶≠аІВа¶Ѓа¶ња¶Ха¶≠а¶Ња¶ђаІЗ а¶ЄаІЛа¶Ьа¶Њ а¶Ха¶∞а¶Њ а¶ѓа¶Ња¶ђаІЗ а¶®а¶Ња•§
а¶Чඌථගටගа¶Х ඙аІНа¶∞а¶Ѓа¶Ња¶£ :
ඁථаІЗ а¶Ха¶∞а¶њ බаІЬа¶ња¶∞ а¶≠а¶∞ඐගථаІНබаІБ а¶Па¶ХаІЗа¶ђа¶Ња¶∞аІЗ බаІЬа¶ња¶∞ а¶Ѓа¶Ња¶Эа¶Ња¶Ѓа¶Ња¶Эа¶ња•§ බаІЬа¶ња¶∞ а¶≠а¶∞ ඃබග m а¶єаІЯ ටඐаІЗ බаІЬа¶ња¶∞ а¶Уа¶Ьථ mg а¶Па¶ђа¶В ටඌ ථගа¶ЪаІЗа¶∞ බගа¶ХаІЗ а¶ХаІНа¶∞а¶њаІЯඌපаІАа¶≤а•§
බаІБа¶З ඙аІНа¶∞ඌථаІНටаІЗа¶∞ а¶ђа¶≤ F а¶Па¶ђа¶В а¶ЭаІБа¶≤аІЗ ඕඌа¶Ха¶Њ බаІЬа¶ња¶∞ ඪඌඕаІЗ а¶ЄаІЛа¶Ьа¶Њ а¶∞аІЗа¶Ца¶Ња¶∞ а¶ХаІЛථ θ
බаІЬа¶ња¶ХаІЗ а¶ЄаІЛа¶Ьа¶Њ а¶ЯඌථටаІЗ а¶єа¶≤аІЗ බаІЬа¶ња¶∞ а¶Уа¶Ьථ а¶Жа¶∞ а¶ђа¶≤аІЗа¶∞(2F) а¶≤а¶ЃаІНа¶ђ а¶Й඙ඌа¶Вප ඪඁඌථ යටаІЗ а¶єа¶ђаІЗа•§
а¶Еа¶∞аІНඕඌаІО, 2F sinθ = mg
F=mg/2sinθ
θ а¶Па¶∞ ඁඌථ а¶ЫаІЛа¶Я а¶єа¶≤аІЗ sin(θ)≈ θ
F= mg/2θ
θ а¶Па¶∞ ඁඌථ 0° а¶єа¶≤аІЗ බаІЬа¶њ а¶ЄаІНа¶ЯаІНа¶∞аІЗа¶За¶Я а¶єа¶ђаІЗа•§ а¶ХගථаІНටаІБ а¶ЄаІЗа¶ХаІНа¶ЈаІЗටаІНа¶∞аІЗ F=mg/2θ а¶П F а¶Па¶∞ ඁඌථ а¶Еа¶ЄаІАа¶Ѓ а¶єаІЯаІЗ а¶ѓа¶Ња¶ђаІЗа•§
а¶Ђа¶≤а¶Ња¶Ђа¶≤, බаІЬа¶ња¶Яа¶Ња¶ХаІЗ а¶ЄаІЛа¶Ьа¶Њ а¶Ха¶∞ටаІЗ а¶єа¶≤аІЗ а¶Еа¶ЄаІАа¶Ѓ а¶ђа¶≤аІЗ а¶ЯඌථටаІЗ а¶єа¶ђаІЗа•§ а¶ХගථаІНටаІБ ටඌ а¶ѓаІЗа¶єаІЗටаІБ а¶Єа¶ЃаІНа¶≠а¶ђ ථඌ ටඌа¶З බаІЬа¶ња¶ХаІЗ а¶ЄаІЛа¶Ьа¶Ња¶У а¶Ха¶∞а¶Њ а¶ѓа¶Ња¶ђаІЗ а¶®а¶Ња•§
а¶ХගථаІНටаІБ а¶ХගථаІНටаІБ  а¶Жа¶Ѓа¶∞а¶Њ а¶ѓаІЗ බаІЗа¶Ца¶њ а¶ЄаІБටඌ а¶Яඌථ බගа¶≤аІЗ ඙аІБа¶∞аІЛ඙аІБа¶∞а¶њ а¶ЄаІЛа¶Ьа¶Њ "බаІЗа¶Ца¶Њ а¶ѓа¶ЊаІЯ"? а¶ЄаІБටඌ පаІБа¶ІаІБ "а¶ЄаІЛа¶Ьа¶Њ බаІЗа¶Ца¶Њ а¶ѓа¶ЊаІЯ", а¶ХගථаІНටаІБ ඙аІНа¶∞а¶ХаІГට඙а¶ХаІНа¶ЈаІЗ ටඌ а¶ЄаІЛа¶Ьа¶Њ ථаІЯа•§ а¶ЄаІБටඌа¶∞ а¶≠а¶∞ а¶Й඙аІЗа¶ХаІНа¶Ја¶£аІАаІЯ а¶ђа¶≤аІЗ а¶ЄаІБටඌа¶∞ а¶ЭаІБа¶≤аІЗ ඕඌа¶Ха¶Ња¶Яа¶Њ а¶Й඙аІЗа¶ХаІНа¶Ја¶£аІАаІЯа•§
а¶Жа¶Ѓа¶∞а¶Њ а¶ѓаІЗ බаІЗа¶Ца¶њ а¶ЄаІБටඌ а¶Яඌථ බගа¶≤аІЗ ඙аІБа¶∞аІЛ඙аІБа¶∞а¶њ а¶ЄаІЛа¶Ьа¶Њ "බаІЗа¶Ца¶Њ а¶ѓа¶ЊаІЯ"? а¶ЄаІБටඌ පаІБа¶ІаІБ "а¶ЄаІЛа¶Ьа¶Њ බаІЗа¶Ца¶Њ а¶ѓа¶ЊаІЯ", а¶ХගථаІНටаІБ ඙аІНа¶∞а¶ХаІГට඙а¶ХаІНа¶ЈаІЗ ටඌ а¶ЄаІЛа¶Ьа¶Њ ථаІЯа•§ а¶ЄаІБටඌа¶∞ а¶≠а¶∞ а¶Й඙аІЗа¶ХаІНа¶Ја¶£аІАаІЯ а¶ђа¶≤аІЗ а¶ЄаІБටඌа¶∞ а¶ЭаІБа¶≤аІЗ ඕඌа¶Ха¶Ња¶Яа¶Њ а¶Й඙аІЗа¶ХаІНа¶Ја¶£аІАаІЯа•§
а¶Жа¶ђа¶Ња¶∞ а¶ђа¶≤а¶њ, а¶≠а¶∞ а¶ѓаІБа¶ХаІНට а¶ХаІЛථ බаІЬа¶ња¶ХаІЗ а¶ЯаІЗථаІЗ а¶Єа¶ЃаІН඙аІБа¶∞аІНа¶£ а¶ЄаІНа¶ЯаІНа¶∞аІЗа¶За¶Я а¶Ха¶∞ටаІЗ а¶єа¶≤аІЗ බаІЬа¶ња¶∞ බаІБа¶З ඙аІНа¶∞ඌථаІНටаІЗ а¶Еа¶ЄаІАа¶Ѓ а¶ђа¶≤ බаІНа¶ђа¶Ња¶∞а¶Њ а¶ЯඌථටаІЗ а¶єа¶ђаІЗа•§а¶Еа¶ЄаІАа¶Ѓ а¶ђа¶≤ බаІНа¶ђа¶Ња¶∞а¶Њ а¶Яඌථඌ а¶ѓаІЗа¶єаІЗටаІБ а¶Єа¶ЃаІНа¶≠а¶ђ ථаІЯ ටඌа¶З, а¶≠а¶∞а¶ѓаІБа¶ХаІНට බаІЬа¶ња¶ХаІЗа¶У а¶Єа¶ЃаІН඙аІБа¶∞аІНථ а¶ЄаІНа¶ЯаІНа¶∞аІЗа¶За¶Я а¶Ха¶∞а¶Њ а¶Єа¶ЃаІНа¶≠а¶ђ ථаІЯа•§
а¶ђа¶ња¶Г බаІНа¶∞а¶Г а¶ђа¶Ња¶єаІБа¶ђа¶≤а¶ња¶∞ ඪගථа¶ЯඌටаІЗ а¶ђа¶Ња¶єаІБа¶ђа¶≤а¶ња¶ХаІЗ а¶Єа¶Ња¶Іа¶Ња¶∞ථ ඁඌථаІБа¶Ј а¶Іа¶∞аІЗ а¶єа¶ња¶ЄаІЗа¶ђ а¶Ха¶∞а¶≤аІЗ ආගа¶Х а¶Жа¶ЫаІЗа•§ а¶ХගථаІНටаІБ а¶ЃаІБа¶≠а¶њ а¶ХаІНа¶ѓа¶Ња¶∞аІЗа¶ХаІНа¶Яа¶Ња¶∞ а¶єа¶ња¶ЄаІЗа¶ђаІЗ а¶Іа¶∞а¶≤аІЗ බаІЬа¶њ а¶Жа¶∞ а¶єа¶Ња¶≤а¶Ха¶Њ а¶Па¶Ха¶ЯаІБ а¶ЄаІЛа¶Ьа¶Њ а¶єа¶УаІЯа¶Њ а¶Йа¶Ъගට( ඙аІБа¶∞аІЛ඙аІБа¶∞а¶њ а¶ЄаІЛа¶Ьа¶Њ ථаІЯ)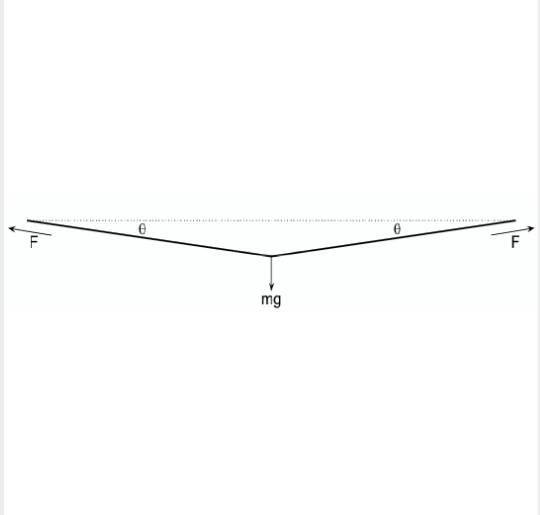
පаІБа¶ІаІБඁඌටаІНа¶∞ а¶За¶ХаІБаІЯаІЗපථ а¶ђаІНа¶ѓа¶ђа¶єа¶Ња¶∞ а¶Ха¶∞а¶ЊаІЯ а¶Па¶ђа¶В а¶Чඌථගටගа¶Х а¶Ђа¶≤а¶Ња¶Ђа¶≤ ථඌ බаІЗаІЯඌටаІЗ а¶Па¶ЦථаІЛ а¶≠ගථаІНථඁට а¶∞аІЯаІЗ а¶ЧаІЗа¶ЫаІЗа•§ а¶ХаІЗа¶Й а¶ђа¶≤а¶ЫаІЗ ඪගථ-а¶Яа¶Њ ආගа¶Ха¶З а¶Жа¶ЫаІЗ а¶Жа¶∞ а¶ХаІЗа¶Й а¶ђа¶≤а¶ЫаІЗ а¶Ђа¶ња¶Ьа¶ња¶ХаІНа¶Є ථඌа¶З а¶єаІЯаІЗ а¶ЧаІЗа¶ЫаІЗа•§ а¶Па¶∞ а¶Па¶Ха¶Яа¶Њ а¶ЄаІБа¶ЈаІНආ ඪඁඌ඲ඌථ а¶Еටග ඙аІНа¶∞аІЯаІЛа¶Ьа¶®а•§
඙аІНа¶∞ඕඁаІЗа¶З බаІЬа¶њ а¶Па¶ђа¶В පа¶ХаІНටගа¶∞ а¶Хඕඌ а¶ђа¶≤аІЗ ථаІЗа¶За•§ ඙а¶≤а¶ња¶Зඕගа¶≤ගථ, ඙а¶≤а¶ња¶Зඕඌа¶За¶≤ගථ а¶ђа¶Њ ථඌа¶За¶≤ථ а¶Па¶∞ ටаІИа¶∞а¶њ 40-50mm а¶ђаІНа¶ѓа¶Ња¶ЄаІЗа¶∞ බаІЬа¶ња¶ЧаІБа¶≤аІЛ 100 а¶Ѓа¶ња¶Яа¶Ња¶∞ а¶П а¶ЧаІЬаІЗ
100kg а¶Па¶∞ ඁටаІЛ а¶єаІЯаІЗ ඕඌа¶ХаІЗа•§ ඙аІНа¶∞ටග а¶Ѓа¶ња¶Яа¶Ња¶∞аІЗ ටඌа¶З 1kg а¶≠а¶∞ а¶Іа¶∞аІЗ а¶єа¶ња¶ЄаІЗа¶ђ а¶Ха¶∞а¶Њ а¶ѓа¶ЊаІЯа•§
඙аІНа¶∞а¶≠а¶Ња¶Є а¶Па¶ђа¶В ටඌа¶∞ ඙аІЗа¶ЫථаІЗа¶∞ а¶≤аІЛа¶ХаІЗа¶∞ බаІБа¶∞ටаІНа¶ђ ඙аІНа¶∞а¶ЊаІЯ аІ®а¶Ѓа¶ња¶Яа¶Ња¶∞аІЗа¶∞ ඁටаІЛа•§
а¶ЄаІЗа¶З а¶єа¶ња¶ЄаІЗа¶ђаІЗ බаІЬа¶ња¶∞ а¶≠а¶∞а¶У 2kg
ඁඌථаІБа¶ЈаІЗа¶∞ а¶Єа¶∞аІНа¶ђаІЛа¶ЪаІНа¶Ъ ඙аІБа¶≤а¶ња¶В а¶ЄаІНа¶ЯаІНа¶∞аІЗа¶Вඕ а¶∞аІЗа¶Ха¶∞аІНа¶° а¶єаІЯаІЗа¶ЫаІЗ 400N.
а¶Па¶ђа¶Ња¶∞ а¶Чඌථගටගа¶Х а¶єа¶Ња¶ђа¶ња¶ЬඌඐගටаІЗ а¶Ъа¶≤аІЗ а¶ѓа¶Ња¶За•§
඙аІНа¶∞а¶≠а¶Ња¶Є а¶Па¶ђа¶В а¶ђа¶Ња¶єаІБа¶ђа¶≤а¶њ බаІБа¶За¶ЬථаІЗа¶∞ а¶ЬථаІНа¶ѓ а¶Жа¶≤ඌබඌа¶≠а¶Ња¶ђаІЗ බаІЬа¶њ а¶Ѓа¶Ња¶Эа¶ЦඌථаІЗ а¶ХටаІЛа¶Яа¶Њ а¶ЭаІБа¶≤аІЗ ඕඌа¶Ха¶ђаІЗ ටඌ а¶ђаІЗа¶∞ а¶Ха¶∞а¶ђаІЈ
඙аІНа¶∞а¶≠а¶Ња¶ЄаІЗа¶∞ а¶ЬථаІНа¶ѓа¶Г
Fsinθ = mg
θ = sinЋЙЋ°(mg/F)
=sinЋЙЋ°(2*9.8/400)
θ= sinЋЙЋ°(0.049)
බаІЬа¶ња¶∞ а¶Ѓа¶Ња¶Эа¶ЦඌථаІЗ а¶Еа¶∞аІНඕඌаІО аІІа¶Ѓа¶ња¶Яа¶Ња¶∞ බаІБа¶∞аІЗ а¶ЭаІБа¶≤а¶ђаІЗ,
sinθ * 1
=sin( sinЋЙЋ°(0.049)) * 1
=0.049m
=4.9 а¶ЄаІЗ.а¶Ѓа¶њ.
පаІБа¶ІаІБ ඙аІНа¶∞а¶≠а¶Ња¶ЄаІЗа¶∞ а¶ЬථаІНа¶ѓ බаІЬа¶ња¶∞ а¶Ѓа¶Ња¶Эа¶ЦඌථаІЗ 4.9а¶ЄаІЗ.а¶Ѓа¶њ. а¶ЭаІБа¶≤а¶ђаІЗа•§ а¶ѓаІЗඁථа¶Яа¶Њ а¶Ђа¶ЯаІЛටаІЗ බаІЗа¶Ца¶Њ а¶ѓа¶ЊаІЯа•§
а¶ђа¶Ња¶єаІБа¶ђа¶≤а¶ња¶∞ а¶ЬථаІНа¶ѓа¶Г
඙аІНа¶∞ඕඁ ඙ඌа¶∞аІНа¶ЯаІЗ ටඌа¶ХаІЗ බаІЗа¶Ца¶Њ а¶ѓа¶ЊаІЯ а¶Па¶Ха¶Яа¶Њ පගඐа¶≤а¶ња¶ЩаІНа¶Ч ටаІБа¶≤аІЗ а¶Ха¶Ња¶Ба¶ІаІЗ ථගටаІЗа¶З а¶ЪаІЗа¶єа¶Ња¶∞а¶Њ а¶ђа¶ња¶ХаІГට а¶єаІЯаІЗ а¶ЧаІЗа¶ЫаІЗа•§ а¶Ра¶∞а¶Ха¶Ѓ а¶Па¶Ха¶Яа¶Њ පගඐа¶≤а¶ња¶ЩаІНа¶ЧаІЗа¶∞ а¶Уа¶Ьථ а¶єа¶ђаІЗ 3000N а¶Па¶∞ а¶Ха¶Ња¶Ыа¶Ња¶Ха¶Ња¶Ыа¶ња•§ а¶Па¶ЬථаІНа¶ѓ ටඌа¶∞ පа¶ХаІНටග а¶Ха¶ња¶ЫаІБа¶Яа¶Њ а¶ђа¶ЊаІЬа¶њаІЯаІЗ 4000N-а¶З а¶Іа¶∞а¶Њ а¶ѓа¶Ња¶Ха•§
θ = sinЋЙЋ°(mg/F)
= sinЋЙЋ° (2*9.8/4000)
= sinЋЙЋ°(0.0049)
а¶Ѓа¶Ња¶Эа¶ЦඌථаІЗ а¶ЭаІЛа¶≤а¶Њ а¶Еа¶Вප,
sin θ * 1
=sin(sinЋЙЋ°(0.0049))*1
=0.0049m
=4.9mm
а¶Еа¶∞аІНඕඌаІО, а¶ђа¶Ња¶єаІБа¶ђа¶≤а¶ња¶∞ а¶ЬථаІНа¶ѓ බаІЬа¶ња¶∞ а¶Ѓа¶Ња¶Эа¶ЦඌථаІЗ 4.9 а¶Ѓа¶ња¶≤а¶ња¶Ѓа¶ња¶Яа¶Ња¶∞ а¶ЭаІБа¶≤аІЗ ඕඌа¶ХටаІЛа•§
4.9cm а¶Па¶ђа¶В 4.9mm